Principal components analysis attempts to find a smaller dimensional subspace that captures the majority of the varation in a dataset. It is a statistical technique that us used in various ways in AI. Witin explainable AI it may be used to help interpret complex data, such as internal layers of a {[deep neural network}}. It can also be used as a dimensional reduction technique during data preparation. One way to calculate the principal components of a data set is first to calcualte the feature cross-correltion matrix, that is the matrix comprising of the correlations between different features. The principal components are then the N eigenvectors with the largest eignevalues. In. particular, the first principal component is the principal eigenvector. One can decide in advance how many principal components are required, or inspect them one by one choosing a point to stop where the eigenvalues drop below a chosen level.
Defined on page 134
Used on Chap. 7: pages 134, 135, 136, 141, 142, 143, 147; Chap. 8: pages 159, 160; Chap. 9: pages 176, 195; Chap. 10: pages 207, 212; Chap. 13: page 313
Also known as principal components
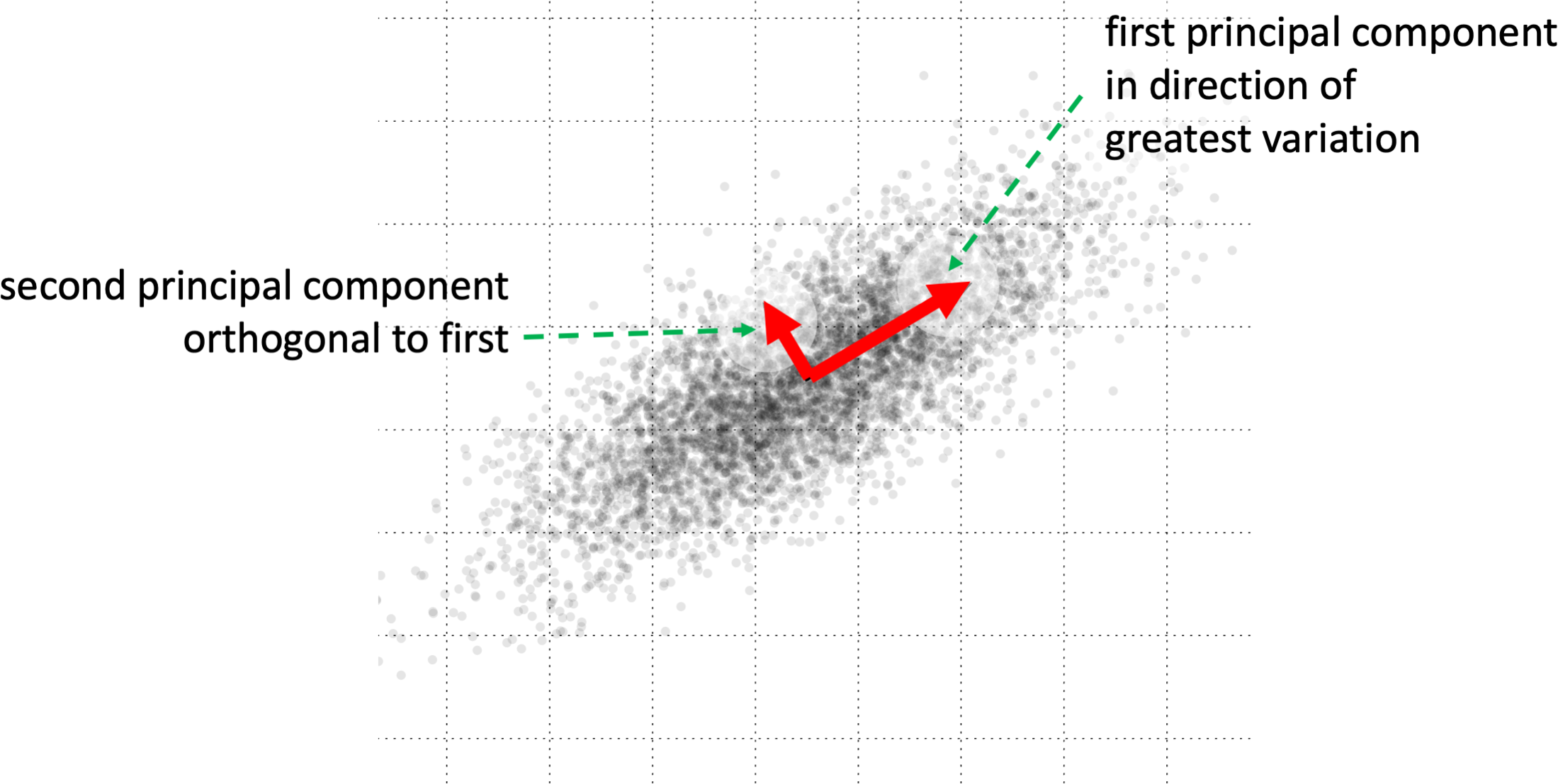
Principal components for 2D data